고정 헤더 영역
상세 컨텐츠
본문
지금까지 다룬 다익스트라나 벨만-포드 알고리즘들은 모두 한 시작점에서 다른 모든 정점까지의 거리를 구해 주었다.
하지만 한 개의 시작점이 아니라 모든 정점 쌍에 둘 사이의 최단 거리를 구해야 할 때도 있다.
이러한 문제를 해결하는 가장 쉬운 방법은 모든 정점으로부터 다익스트라 알고리즘을 적용하면 되는 것이다.
만약 음수 가중치가 있다면 벨만 포드 알고리즘을 사용하면 된다.
그러나 이것보다 좀 더 빠르고 간단한 방법이 있다. 그것은 이제 설명할 플로이드 워셜(Floyd-Warshall) 알고리즘이다.
플로이드 워셜 알고리즘은 모든 정점 쌍의 최단 거리를 저장하는 2차원 배열 dist[][]를 계산한다.
이 배열의 원소 dist[u][v]는 정점 u에서 v로 가는 최단 거리를 나타낸다.
정점의 경유점들
우선 플로이드 워셜의 동작 과정을 이해하기 위해서는 경로의 경유점의 개념을 소개할 필요가 있다.
두 정점 u, v를 잇는 어떤 경로가 있다고 가정해보자. 이때, u와 v는 시작과 끝점을 의미한다. 그리고 경로는 항상 시작점 u 와 끝점 v를 지난다. 이 외에 이 경로는 다른 정점들을 지나쳐갈 수도 있다. 이와 같이 경로가 거쳐가는 정점들을 경유점이라고 하자.

위의 그림을 보도록 하자.
정점 집합 S에 포함된 정점만을 경유점으로 사용해 u에서 v로 가는 최단 경로의 길이를 DS(u, v)라고 표기하도록 한다.
위의 그림에서는 D{}(a, b) = 5 이지만 D{c, d}(a, b) = 4 이다. 하지만 이 정점들을 굳이 모두 이용할 필요는 없다. 다음과 같이 D{a, c, d, e, g, f}(b, f) = D{}(b, f) = 3 이다.
즉, 이 표기법을 쓸 때 최종적으로 우리가 계산하고 싶은 값은 전체 정점의 집합 V를 모두 경유점으로 쓸 수 있는 DV이고, 두 정점 사이를 잇는 간선 중 가장 짧은 간선의 길이 w(u, v)는 D{}(u, v)가 된다는 것을 알 수 있다.
정점 S에 포함된 정점만을 경유점으로 사용하여 u에서 v로 가는 최단 거리를 알고 있다고 하자. 그럼 S 중에 하나의 정점을 x라고 했을 경우 최단 경로는 이를 경유할 수도 있고, 아닐 수도 있다.
각 경우에 따라 최단 경로는 다음의 두 가지 모습으로 나타날 수 있다.
- x를 경유하지 않는 경우
이 경로는 S - {x}에 포함된 정점들만을 경유점으로 사용한다. - x를 경유하는 경우
u에서 x로 그리고 x에서 v로 가는 구간으로 나눌 수 있다. 이 두 개의 부분 경로들은 각각 u와 x, x 와 v를 잇는 최단 경로들이어야 한다. 당연하게도 두 개의 부분 경로는 x를 경유하지 않으므로 S - {x}에 포함된 정점들만을 경유점으로 사용한다.
그럼 최단 경로는 둘 중 더 짧은 경로가 되므로 이를 다음과 같이 재귀적으로 정의할 수 있게 된다.

점화식 그대로 코드에 옮기기
위의 점화식을 아래와 같이 살짝 고쳐서 사용해보도록 하자.
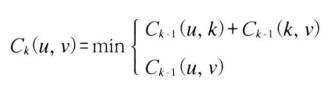
C[k](u, v)는 0번 정점부터 k번 정점까지만을 경유점으로 썼을 때 u에서 v까지 가는 최단 경로의 길이가 된다.
이 점화식에서 C[k]의 모든 값은 C[k - 1]에만 의존하기 때문에, 반복적 동적 계획법을 이용하면 쉽게 풀 수 있다.
이 코드에서 C[k](u, v)의 값은 C[k][u][v]에 저장된다. 따라서 종료 후에 u에서 v로 가는 최단 경로를 보기 위해서는 C[V - 1][u][v]의 값을 보면 된다.
// 정점의 개수
int V;
// 그래프의 인접 행렬 표현
// adj[u][v] = u 에서 v로 가는 간선의 가중치, 간선이 없으면 아주 큰 값을 넣는다.
int adj[MAX_V][MAX_V];
int C[MAX_V][MAX_V][MAX_V];
void allPairShortestPath1()
{
// C[0]를 초기화
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
if (i != j)
c[0][i][j] = min(adj[i][j], adj[i][0] + adj[0][j]);
else
c[0][i][j] = 0;
}
}
// C[k - 1]이 있으면 C[k]를 계산할 수 있다.
for (int k = 1; k < V; k++)
{
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
C[k][i][j] = min(C[k - 1][i][j],
C[k - 1][i][k] + C[k - 1][k][j]);
}
}
}
이 알고리즘의 시간 복잡도는 O(|V|^3)이 된다.
메모리 사용량 줄이기
사실 이 알고리즘의 문제는 메모리의 크기가 너무나도 커질 수도 있다는 것이다.
물론 이 알고리즘에서 C[k]의 답은 C[k - 1]만 있으면 되기 때문에 슬라이딩 윈도우 기법을 이용하면 배열의 크기를 O(|V|^2)로 줄일 수 있다.
이 점을 이용하면 배열 크기를 2 * |V| * |V|로 줄일 수 있게 된다. 그야 C[k]의 값을 C[k % 2][u][v]에 저장하면 그만이기 때문이다.
하지만 이보다 더 좋은 방법이 있다.
바로 별도의 배열을 사용하지 않고 그래프의 가중치를 담는 adj[][]배열에서 이 점화식의 결과를 계산하는 것이다.
이것이 어떻게 가능할까?
위의 점화식을 자세히 보도록하자.
C[k](u, v)를 계산하기 위해서는 C[k - 1](u, k)와 C[k - 1][k][v]만 사용하는 것을 알 수 있다.
그럼 C[k](u, k)와 C[k - 1](u, k)는 얼마나 다를까?
- C[k - 1](u, k) = 시작점부터 k - 1번 정점까지를 경유점으로 이용해 u 에서 k로 가는 최단 경로의 길이
- C[k](u, k) = 시작점부터 k번 정점까지를 경유점으로 이용해 u에서 k로 가는 최단 경로의 길이
이를 보면 알 수 있지만, 출발점이나 도착점이 k번 정점일 때 사용 가능한 경유점의 목록에 k가 추가되는 것은 아무런 의미가 없다.
그렇기 때문에 굳이 C[k % 2]와 C[(k - 1) % 2]를 구분할 필요가 없기 때문에 한 개의 2차원 배열에 섞어 써도 된다.
이렇게 하여 시간 복잡도는 그대로지만 공간 복잡도는 O(|V|^2)로 줄어들었다.
// 플로이드의 모든 쌍 최단 거리 알고리즘
void floyd()
{
for (int i = 0; i < V; i++)
adj[i][i] = 0;
for (int k = 0; k < V; k++)
{
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
adj[i][j] = min(adj[i][j], adj[i][k] + adj[k][j]);
}
}
}
플로이드 알고리즘의 최적화
이 알고리즘은 한 10%에서 20%는 정도 그래프에 간선이 적을수록 효과가 좋은 최적화 기법이 있다.
바로 두 번째 for문 바로 다음에 i에서 k로 가는 경로가 실제 있는지를 확인해 보는 것이다. 만약 i에서 k로 가는 경로가 없다면 j에 대한 for문은 수행할 필요가 없기 때문이다.
'알고리즘 > 이론' 카테고리의 다른 글
| 벨만 포드 알고리즘(Bellman-Ford Algorithm) (0) | 2023.05.23 |
|---|---|
| BFS는 왜 가중치가 있는 그래프에서 사용할 수 없을까? (1) | 2023.05.21 |
| 다익스트라(Dijkstra) 알고리즘 (0) | 2023.05.21 |
| 트리의 지름 증명 (0) | 2023.05.20 |




